Definisi Kaedah Regresi Kuadrat Kurang
Kaedah regresi kuasa dua adalah bentuk analisis regresi yang mewujudkan hubungan antara pemboleh ubah bersandar dan bebas bersama dengan garis linear. Garis ini disebut sebagai "garis yang paling sesuai."
Analisis Regresi adalah kaedah statistik dengan bantuan yang mana seseorang dapat menganggarkan atau meramalkan nilai yang tidak diketahui dari satu pemboleh ubah dari nilai yang diketahui dari pemboleh ubah lain. Pemboleh ubah yang digunakan untuk meramalkan pemboleh ubah minat disebut pemboleh ubah bebas atau penjelasan, dan pemboleh ubah yang sedang diramalkan disebut pemboleh ubah bersandar atau dijelaskan.
Mari kita pertimbangkan dua pemboleh ubah, x & y. Ini dilakarkan pada graf dengan nilai x pada nilai paksi-x dari y pada paksi-y. Nilai-nilai ini ditunjukkan oleh titik-titik dalam grafik di bawah. Garis lurus dilukis melalui titik - disebut sebagai garis paling sesuai.

Objektif regresi kuadrat terkecil adalah untuk memastikan bahawa garis yang dilukis melalui set nilai yang disediakan mewujudkan hubungan yang paling dekat antara nilai.
Formula Regresi Kuadrat Kurang
Garis regresi di bawah kaedah Least Squares dikira menggunakan formula berikut -
ŷ = a + bx
Di mana,
- ŷ = pemboleh ubah bersandar
- x = pemboleh ubah bebas
- a = pintasan-y
- b = cerun garisan
Cerun garis b dikira menggunakan formula berikut -

Atau

Pintasan-Y, 'a' dikira menggunakan formula berikut -

Garis Kesesuaian Terbaik di Regresi Least Square
Garis paling sesuai adalah garis lurus yang dilukis melalui sebaran titik data yang paling mewakili hubungan antara mereka.
Mari kita perhatikan grafik berikut di mana sekumpulan data diplotkan sepanjang paksi x dan y. Titik data ini dilambangkan menggunakan titik biru. Tiga garis dilukis melalui titik-titik ini - garis hijau, merah, dan biru. Garis hijau melewati satu titik, dan garis merah melewati tiga titik data. Walau bagaimanapun, garis biru melewati empat titik data, dan jarak antara titik baki ke garis biru adalah minimum berbanding dengan dua garis lain.

Dalam grafik di atas, garis biru mewakili garis paling sesuai kerana terletak paling dekat dengan semua nilai dan jarak antara titik di luar garis ke garis adalah minimum (iaitu, jarak antara baki ke garis paling sesuai - juga disebut sebagai jumlah petak sisa). Dalam dua garis lain, oren dan hijau, jarak antara baki ke garis lebih besar jika dibandingkan dengan garis biru.
Kaedah kuasa dua memberikan hubungan yang paling dekat antara pemboleh ubah bersandar dan bebas dengan meminimumkan jarak antara sisa, dan garis paling sesuai, iaitu, jumlah petak sisa adalah minimum di bawah pendekatan ini. Oleh itu istilah "petak paling sedikit."
Contoh Garisan Regresi Kuadrat Kurang
Mari kita gunakan formula ini dalam soalan di bawah -
Contoh # 1
Perincian berkaitan dengan pengalaman juruteknik di sebuah syarikat (dalam beberapa tahun) dan penilaian prestasi mereka diberikan dalam jadual di bawah. Dengan menggunakan nilai-nilai ini, anggarkan penilaian prestasi untuk juruteknik dengan pengalaman 20 tahun.
| Pengalaman Juruteknik (dalam Tahun) | Penilaian Prestasi |
| 16 | 87 |
| 12 | 88 |
| 18 | 89 |
| 4 | 68 |
| 3 | 78 |
| 10 | 80 |
| 5 | 75 |
| 12 | 83 |
Penyelesaian -
Untuk mengira kuasa dua terkecil pertama kita akan mengira pintasan-Y (a) dan cerun garis (b) seperti berikut -

Cerun Garisan (b)

- b = 6727 - ((80 * 648) / 8) / 1018 - ((80) 2 /8)
- = 247/218
- = 1.13
Pintasan-Y (a)

- a = 648 - (1.13) (80) / 8
- = 69.7
Garis regresi dikira seperti berikut -

Mengganti 20 untuk nilai x dalam formula,
- ŷ = a + bx
- ŷ = 69.7 + (1.13) (20)
- ŷ = 92.3
Peringkat prestasi untuk juruteknik dengan pengalaman 20 tahun dianggarkan 92.3.
Contoh # 2
Persamaan Regresi Kuadrat Kurang Menggunakan Excel
Persamaan regresi kuasa dua paling sedikit dapat dihitung menggunakan excel dengan langkah-langkah berikut -
- Masukkan jadual data di excel.

- Masukkan graf penyebaran menggunakan titik data.

- Masukkan garis arah aliran dalam graf penyebaran.

- Di bawah pilihan garis trend - pilih garis arah linear dan pilih persamaan paparan pada carta.

- Persamaan regresi kuasa dua paling sedikit untuk set data excel yang diberikan ditunjukkan pada carta.
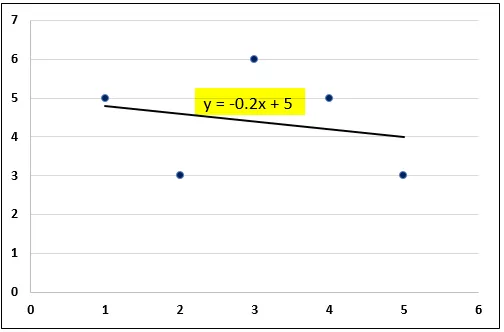
Oleh itu, persamaan regresi kuasa dua terkurang untuk set data excel yang diberikan dikira. Dengan menggunakan persamaan, ramalan, dan analisis trend boleh dibuat. Alat Excel juga menyediakan pengiraan regresi terperinci.
Kelebihan
- Kaedah analisis regresi kuasa dua paling sesuai untuk model ramalan dan analisis trend. Ia paling baik digunakan dalam bidang ekonomi, kewangan, dan pasaran saham di mana nilai mana-mana pemboleh ubah masa depan diramalkan dengan bantuan pemboleh ubah yang ada dan hubungan antara yang sama.
- Kaedah kuasa dua memberikan hubungan terdekat antara pemboleh ubah. Perbezaan antara jumlah petak sisa hingga garis paling sesuai adalah minimum di bawah kaedah ini.
- Mekanisme pengiraannya mudah dan senang digunakan.
Kekurangan
- Kaedah kuadrat paling kecil bergantung pada menjalin hubungan terdekat antara satu set pemboleh ubah yang diberikan. Mekanisme pengiraan sensitif terhadap data, dan sekiranya terdapat outliers (data luar biasa), hasilnya cenderung mempengaruhi.
- Jenis pengiraan ini sangat sesuai untuk model linear. Untuk persamaan tidak linear, mekanisme pengiraan yang lebih lengkap digunakan.
Kesimpulannya
Kaedah kuadrat terkecil adalah salah satu kaedah yang paling popular digunakan untuk model ramalan dan analisis trend. Apabila dikira dengan tepat, ia memberikan hasil terbaik.








