Apakah Pekali Korelasi?
Pekali korelasi digunakan untuk menentukan seberapa kuat hubungan antara dua pemboleh ubah dan nilainya dapat berkisar antara -1.0 hingga 1.0, di mana -1.0 mewakili korelasi negatif dan +1.0 mewakili hubungan positif. Ia mempertimbangkan pergerakan relatif dalam pemboleh ubah dan kemudian menentukan jika ada hubungan antara mereka.
Formula Pekali Korelasi
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Di mana
- r = pekali korelasi
- n = bilangan pemerhatian
- x = 1 st berubah-ubah dalam konteks
- y = pemboleh ubah 2 nd
Penjelasan
Sekiranya ada korelasi atau mengatakan hubungan antara dua pemboleh ubah, maka itu akan menunjukkan jika salah satu pemboleh ubah berubah dalam nilai, maka pemboleh ubah yang lain juga cenderung berubah nilai, katakan secara spesifik yang dapat sama atau sama arah yang bertentangan. Bahagian pengangka dari persamaan melakukan ujian dan kekuatan relatif pemboleh ubah bergerak bersama, dan bahagian penyebut dari persamaan menimbang pengangka dengan mengalikan perbezaan pemboleh ubah dari pemboleh ubah kuasa dua.
Contoh
Contoh # 1
Pertimbangkan dua pemboleh ubah berikut, x, dan y, anda diminta untuk mengira pekali korelasi.
Di bawah ini diberikan data untuk pengiraan.

Penyelesaian:
Dengan menggunakan persamaan di atas, kita dapat mengira yang berikut

Kami mempunyai semua nilai dalam jadual di atas dengan n = 4.
Mari kita masukkan nilai untuk pengiraan pekali korelasi.

Oleh itu, pengiraannya adalah seperti berikut,

r = (4 * 25,032.24) - (262.55 * 317.31) / √ ((4 * 20.855.74) - (262.55) 2 ) * ((4 * 30.058.55) - (317.31) 2 )
r = 16,820.21 / 16,831.57
Pekali akan -

Pekali = 0.99932640
Contoh # 2
Negara X adalah negara ekonomi yang sedang berkembang, dan ia ingin melakukan analisis bebas terhadap keputusan yang diambil oleh bank pusatnya mengenai perubahan kadar faedah, sama ada yang mempengaruhi inflasi dan bank pusat dapat mengendalikan hal yang sama.
Berikut ringkasan kadar faedah dan kadar inflasi yang berlaku di negara ini secara rata-rata untuk tahun-tahun tersebut diberikan di bawah.
Di bawah ini diberikan data untuk pengiraan.

Presiden negara telah mendekati anda untuk melakukan analisis dan memberikan pembentangan mengenai perkara yang sama dalam pertemuan berikutnya. Gunakan korelasi dan tentukan sama ada bank pusat telah memenuhi objektifnya atau tidak.
Penyelesaian:
Dengan menggunakan formula yang dibincangkan di atas, kita dapat mengira pekali korelasi. Memperlakukan kadar faedah sebagai satu pemboleh ubah, katakanlah x, dan memperlakukan kadar inflasi sebagai pemboleh ubah lain sebagai y.

Kami mempunyai semua nilai dalam jadual di atas dengan n = 6.
Mari kita masukkan nilai untuk pengiraan pekali korelasi.


r = (6 * 170.91) - (46.35 * 22.24) / √ ((6 * 361.19) - (46.35) 2 ) * ((6 * 82.74) - (22.24) 2 )
r = -5.36 / 5.88
Korelasi akan -

Korelasi = -0.92
Analisis: Nampaknya korelasi antara kadar faedah dan kadar inflasi adalah negatif, yang nampaknya merupakan hubungan yang betul. Ketika suku bunga meningkat, inflasi menurun, yang berarti mereka cenderung bergerak ke arah yang berlawanan antara satu sama lain, dan dari hasil di atas menunjukkan bahawa bank pusat berjaya melaksanakan keputusan yang berkaitan dengan kebijakan suku bunga.
Contoh # 3
Makmal ABC sedang menjalankan penyelidikan mengenai ketinggian dan usia dan ingin mengetahui apakah ada hubungan antara mereka. Mereka telah mengumpulkan sampel 1000 orang untuk setiap kategori dan mendapat ketinggian rata-rata dalam kumpulan itu.
Di bawah ini diberikan data untuk pengiraan pekali korelasi.

Anda diminta untuk mengira pekali korelasi dan membuat kesimpulan bahawa jika ada hubungan.
Penyelesaian:
Merawat Umur sebagai satu pemboleh ubah, katakanlah x, dan merawat tinggi (dalam cms) sebagai pemboleh ubah lain sebagai y.

Kami mempunyai semua nilai dalam jadual di atas dengan n = 6.
Mari kita masukkan nilai untuk pengiraan pekali korelasi.

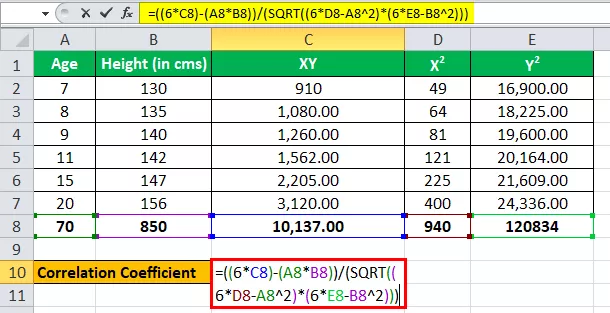
r = (6 * 10,137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20,834) - (850) 2 )
r = 1,322.00 / 1,361.23
Korelasi akan -

Korelasi = 0.971177099
Perkaitan dan Penggunaan
Ia digunakan dalam statistik terutamanya untuk menganalisis kekuatan hubungan antara pemboleh ubah yang sedang dipertimbangkan dan selanjutnya ia juga mengukur jika ada hubungan linear antara kumpulan data yang diberikan dan seberapa baik hubungannya. Salah satu ukuran biasa yang digunakan dalam korelasi adalah pekali korelasi Pearson.
Sekiranya pemboleh ubah berubah dalam nilai dan seiring dengan perubahan nilai yang lain, maka memahami hubungan itu sangat penting kerana seseorang dapat menggunakan nilai pemboleh ubah sebelumnya untuk meramalkan perubahan nilai pemboleh ubah yang terakhir. Korelasi mempunyai banyak kegunaan hari ini di era moden ini seperti yang digunakan dalam industri kewangan, penyelidikan ilmiah, dan di mana tidak. Tetapi, penting untuk mengetahui bahawa korelasi mempunyai tiga jenis hubungan utama. Yang pertama adalah hubungan positif, yang menyatakan jika ada perubahan pada nilai pemboleh ubah, maka akan ada perubahan pada pemboleh ubah yang berkaitan dalam arah yang sama. Begitu juga, jika ada hubungan negatif, maka pemboleh ubah yang berkaitan akan berperilaku ke arah yang berlawanan. Juga, jika tidak ada korelasi, maka r akan menunjukkan nilai sifar.Lihat gambar di bawah untuk lebih memahami konsep.